Conic Sections: A Journey Through History
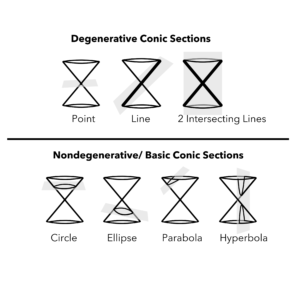
Conic sections are among the most important and enduring concepts in mathematics, with applications spanning from geometry and physics to astronomy and engineering. These shapes, which include circles, ellipses, parabolas, and hyperbolas, arise from the intersection of a plane and a double-napped cone. The development of the theory of conic sections was a collaborative effort that spanned centuries, with contributions from some of the most influential mathematicians in history.
Origins of Conic Sections: Ancient Greece
The concept of conic sections can be traced back to ancient Greece. The earliest recorded work on conic sections was by Menaechmus, a student of the famous Greek philosopher Plato, around 350 BCE. Menaechmus is often credited with discovering conic sections while attempting to solve the problem of duplicating the cube, which involved finding the side length of a cube that has twice the volume of a given cube. His work laid the groundwork for understanding the geometric properties of these curves. Menaechmus described the curves as the intersections of a plane with a cone, producing three distinct types of curves: the ellipse, the parabola, and the hyperbola.
Menaechmus’s discovery was a major breakthrough in Greek mathematics, but it lacked a formal classification and rigorous treatment. His work was later expanded upon by other Greek mathematicians, most notably Euclid and Apollonius of Perga.
Euclid and the Formalization of Geometry
Euclid, widely regarded as the “Father of Geometry,” made significant contributions to the study of conic sections through his work in the Elements, written around 300 BCE. Although Euclid did not specifically focus on conic sections, his systematic approach to geometry laid the foundation for future mathematicians to explore these curves in greater detail. Euclid’s postulates and axioms provided a rigorous framework for understanding geometric shapes, and his influence on conic sections can be seen in the way later mathematicians approached the subject.
Euclid’s contribution to conic sections was more implicit than direct, but his influence on the development of mathematical rigor cannot be understated. His approach to geometry helped solidify the study of conic sections as a legitimate branch of mathematics.
Apollonius of Perga: The “Great Geometer”
The most significant advances in the study of conic sections were made by Apollonius of Perga around 200 BCE. Apollonius’s work on conic sections is considered one of the greatest achievements in Greek mathematics. He wrote an eight-volume treatise titled Conics, in which he systematically developed the theory of conic sections, giving them the names we still use today: ellipse, parabola, and hyperbola. Apollonius’s work built upon the discoveries of Menaechmus and Euclid, but he took the subject much further by introducing new terminology and methods of analysis.
Apollonius’s Conics was groundbreaking in its use of a more algebraic approach to describe the properties of conic sections, moving beyond the purely geometric methods of his predecessors. He explored how conic sections could be generated by varying the angle at which a plane intersects a cone and provided detailed descriptions of their properties. His work also introduced the concept of asymptotes for hyperbolas, a feature that would later become important in calculus and analytical geometry.
Apollonius’s work was so advanced that it remained the standard reference on conic sections for centuries, influencing mathematicians well into the Renaissance and beyond. The Conics not only contributed to pure mathematics but also had practical applications in astronomy, where the orbits of planets could be modeled using ellipses.
The Revival of Conic Sections: The Islamic Golden Age
After the decline of the Roman Empire, much of the knowledge of conic sections was preserved and further developed by Islamic mathematicians during the Islamic Golden Age (8th to 14th centuries). One of the most notable figures in this period was Al-Khwarizmi, a Persian mathematician who contributed to the spread of Greek mathematics through his translations of Greek texts into Arabic. These translations included the works of Euclid and Apollonius, which were studied and expanded upon by mathematicians in the Islamic world.
During this period, conic sections were applied to problems in astronomy and optics. Ibn al-Haytham (known as Alhazen in the West), a prominent mathematician and physicist, used conic sections to study the reflection of light in mirrors with curved surfaces. His work in optics was a precursor to the later development of lenses and telescopes, illustrating the practical applications of conic sections beyond pure mathematics.
Renaissance and the Birth of Analytical Geometry
The Renaissance marked a period of renewed interest in classical mathematics, including conic sections. One of the key figures in the revival of conic sections during this time was the French mathematician and philosopher René Descartes. In the 17th century, Descartes developed analytical geometry, which allowed mathematicians to describe geometric shapes using algebraic equations. This new approach revolutionized the study of conic sections, making it possible to analyze them using coordinates and equations rather than purely geometric methods.
Descartes’s work laid the foundation for the later development of calculus and provided a more powerful tool for studying conic sections. For example, the equation for a circle can be written as x2+y2=r2, where r is the radius of the circle. Similarly, the equations for parabolas, ellipses, and hyperbolas could now be expressed algebraically, allowing for a deeper understanding of their properties and applications.
Johannes Kepler and the Elliptical Orbits of Planets
In the early 17th century, the German mathematician and astronomer Johannes Kepler made a groundbreaking discovery related to conic sections. Using data collected by his mentor Tycho Brahe, Kepler formulated his three laws of planetary motion, which describe the orbits of planets around the sun. Kepler’s first law states that the orbits of planets are ellipses, with the sun at one focus. This was a revolutionary idea that challenged the long-held belief in circular orbits, which had dominated astronomy since the time of Ptolemy.
Kepler’s use of ellipses to describe planetary orbits demonstrated the practical significance of conic sections in understanding the physical world. His work laid the foundation for Isaac Newton’s theory of gravitation and remains one of the most important applications of conic sections in the history of science.
Isaac Newton and the Calculus of Conic Sections
In the late 17th century, Isaac Newton built upon the work of Kepler and Descartes by developing the calculus of conic sections. Newton’s Principia Mathematica, published in 1687, included a detailed analysis of conic sections in the context of his laws of motion and universal gravitation. Newton showed that the orbits of planets and other celestial bodies could be described by conic sections under the influence of gravity.
Newton’s work in calculus and conic sections provided a unified mathematical framework for understanding the motion of objects in the universe. His contributions further cemented the importance of conic sections in both mathematics and physics, influencing generations of scientists and mathematicians to come.
Conclusion
Conic sections have a long and rich history, with contributions from some of the greatest minds in mathematics and science. From the early work of Menaechmus and Apollonius to the revolutionary discoveries of Kepler and Newton, conic sections have played a central role in the development of mathematics, astronomy, and physics. The study of these curves continues to be important today, with applications in areas as diverse as engineering, architecture, and space exploration.
The journey of conic sections through history is a testament to the enduring power of mathematics to describe and explain the natural world. As we continue to explore new frontiers in science and technology, conic sections remain a fundamental tool in our understanding of the universe.
Please Visit Our Sponsors:
We only support vendors that we use ourselves in our home. The links below are our own links or affiliate links but know that we use all of these now, or have in the past. As the author/creator of this blog, I also tutor mathematics on Wyzant, sell on Etsy, create content on TpT, and learn Korean on Rosetta Stone.